Dominanten und die Sixte ajoutée

von Ulrich Kaiser

(Rameauscher Quintsextakkord)

Jean-Philippe Rameau war ein berühmter französischer Komponist, Musiktheoretiker und einer der Gründungsväter unserer heutigen Harmonielehre. Jean-Baptiste le Rond d’Alembert, der als Mathematiker, Physiker und Philosoph ein großes Interesse an wissenschaftlichen Überlegungen hatte, schätzte Rameaus Theorie zur Musik und begann ab 1752, sich für das theoretische Werk Rameaus einzusetzen. Eine seiner Schriften hat der Komponisten und Musiktheoretiker Friedrich Wilhelm Marpurg ins Deutsche übersetzt (Systematische Anleitung in die musicalische Setzkunst, Leipzig 1757) und mit Anmerkungen versehen. Marpurg erklärt hier die Bedeutung des Quintesextakkords für die Theorie Rameaus durch ein Notenbeispiel:

Er verweist darauf, dass der »Verfasser« (Jean-Philippe Rameau) eine Unterscheidung zwischen zwei Akkorden trifft, die im Generalbass beide als »Sextquintenaccorde« beziffert und bezeichnet werden. Das folgende Notenbeispiel zeigt die Beispiele Marpurgs in moderner Notation:

Für diese Unterscheidung ist wichtig zu verstehen, was Rameau unter einer Dominante (auch in seinen Schriften franz. »Dominante«) verstanden hat: Als Dominante bezeichnet Rameau Akkorde, die durch die charakteristische Dissonanz der Septime gekennzeichnet sind, welche sich stufenweise abwärts auflösen muss bei gleichzeitigem Quintfall im Fundament (als Fundament wird der Grundton eines Akkordes bezeichnet, der nicht mit dem Basston identisch sein muss). Nimmt man beispielsweise einen C-Dur-Akkord und fügt ihm eine Septime hinzu, wird dieser zu einer Dominante, wobei sich die Septime h in das a eines Akkordes mit dem Fundament f auflöst:

Aufgabe 1

Löse die folgenden Akkorde als Dominanten im Sinne Rameaus auf:

Aufgabe 2

Studieren Sie die wichtige Stelle zum Sixte ajoutée im Original:

Historisch gesehen haben sich die Septimenakkorde aus einer Durchgangsdissonanz entwickelt, wobei sich die ursprünglich auf metrisch leichterer Zeit erklingende Intervalldissonanz zum Bestandteil einer Akkorddissonanz (Septimenakkord) entwickelt hat:

Das Musterbeispiel für eine Akkordfolge, die nur aus Dominanten besteht, ist die Quintfallsequenz. In ihr ist idealer Weise jeder Akkord durch die charakteristische Dissonanz der Septime gekennzeichnet, alle Septimen lösen sich stufenweise abwärts auf und die Fundamente der Akkorde bilden eine Kette aus ausschließlich fallenden Quinten (bzw. steigenden Quarten):

Aufgabe 3

Schreibe von den gegebenen Anfangsakkorde der I. Stufe eine Quintfallseqenz, bis die erste Stufe wieder erreicht ist:

Dass Rameau jeden Septakkord als Dominante (also auch Nebenseptakkorde) bezeichnet hat, unterscheidet seine Auffassung des Begriffs Dominante von unserem heutigen Verständis. Denn üblicher Weise verstehen wir unter Dominante nur den Septakkord der V. Stufe (Dominantseptakkord), den Rameau als eine Sonderform der Dominante mit dem Zusatz »tonique« versehen hat (Dominante-tonique = Dominantseptakkord / Dominante = alle Septakkorde). Von einer Dominante unterscheidet Rameau grundsätzlich die Subdominante (»Sousdominante«). Als Subdominante werden Akkorde bezeichnet, die durch die charakteristische Dissonanz der großen Sexte (›Sixte ajoutée‹) gekennzeichnet sind, welche sich stufenweise aufwärts auflösen muss bei gleichzeitigem Quartfall im Fundament. Nimmt man beispielsweise einen C-Dur-Akkord und fügt ihm eine Sixte ajoutée hinzu, wird dieser zu einer Subdominante, wobei sich die Sexte a in das h eines Akkordes mit dem Fundament g auflöst:

Aufgabe 4

Löse die folgenden Akkorde als Subdominanten im Sinne Rameaus auf:

                       

Auch die Sixte ajoutée ist historisch gesehen aus einer Durchgangsdissonanz entstanden, wobei wobei sich die ursprünglich auf metrisch leichterer Zeit erklingende Intervalldissonanz zum Bestandteil einer Akkorddissonanz (Akkord mit hinzugefügter großer Sexte) entwickelt hat:

Verbindet man Subdominanten im Sinne Rameaus zu einer Akkordfolge, entsteht eine Quintanstiegssequenz, deren Fundamentstimme sich als Fortschreitung aus Quintstiegen (bzw. Quartfällen) beschreiben lässt:

Aufgabe 5

Schreibe von den gegebenen Anfangsakkorde der I. Stufe eine Quintanstiegssequenz, bis die dritte Stufe erreicht ist:

Der Abschluss einer Quintfallsequenz (VI−II−V−I) lässt sich als Kadenz gestalten. Chiffriert man den Septakkord der II. Stufe (d−f−a−c) mit Hilfe von Funktionssymbolen, läge die folgende Chiffrierung nahe:

Das Problem entsteht bei der Chiffrierung der gleichen Wendung in Moll, denn hier ist der Septakkord der II. Stufe (d−f−as−c) ein halbverminderter Septakkord, der sich angemessen weder als Parallele noch als Gegenklang der Subdominante chiffrieren lässt:

Um nicht Gleiches (II−V−I-Kadenz) in Dur und Moll verschieden kennzeichnen zu müssen, hat sich sowohl für Dur als auch für Moll die folgende funktionstheoretische Chiffrierung durchgesetzt:

Doch was im Sinne der Funktionstheorie richtig und nachvollziehbar ist, muss aus der Sicht Rameaus als falsch bezeichnet werden, da den Akkorden d−f−a−c und d−f−as−c in der authentischen Kadenz jeweils ein G-Dur-Akkord folgt, weshalb Rameau diese Akkorde als Dominanten mit charakteristischer Septimdissonanz (c) verstanden und die Verbindung durch den Fundamentschritt (d−g) beschrieben hätte. Nur in den folgenden plagalen Wendungen wären nach Rameau die Akkorde d−f−a−c und d−f−as−c als Subdominaten bzw. als Akkorde mit Sixte ajoutée anzusehen:

Aufgabe 6

Chiffriere die gegebenen Akkordfolgen sowohl mit Stufenzeichen (über dem System) als auch mit Funktionssymbolen (unter dem System):

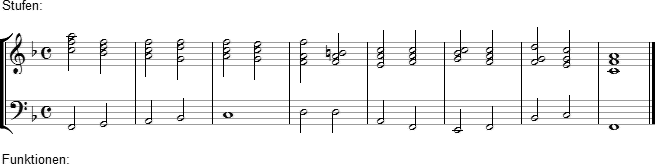
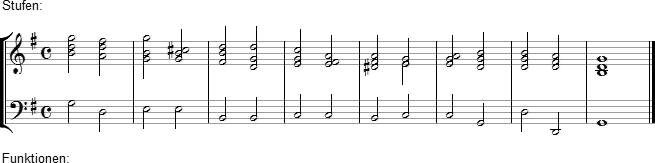
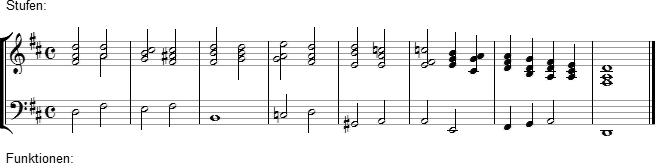
Tabelle zur Funktionstheorie (in Arbeit)

Im 18. Jahrundert hat man nicht nur plagale Wendungen, sondern auch Verbindungen, die wir heute kontrapunktisch erklären würden, als Akkordsatz interpretiert. In dem nächsten Beispiel wäre es zum Beispiel denkbar, die Töne d (Bass) und f (Alt) als Durchgangstöne zwischen Grundton und Terz (c−e) bzw. zwischen Terz und Quintton (e−g) eines C-Dur-Akkords aufzufassen. Rameau hätte diese Wendung als Zusammensetzung aus drei Akkorde verstanden: Zwei Akkorde mit dem Fundament c sind durch eine Subdominante mit dem Fundament f und der Sixte ajoutée d im Bass verbunden:

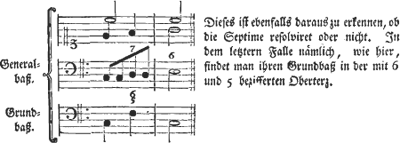
Das nächste Notenbeispiel zeigt das Beispiel aus den Kommentaren Marpurgs zu »den Lehrsätzen des Herrn Rameau« in moderner Notation:

Im 19. Jahrundert kommen Alterationen des Rameauschen Quintsextakkordes bzw. der Sixte ajoutée vor. Durch Alteration der Sexte entsteht ein übermäßiger Quintsextakkord, der sich traditioneller Weise in eine Dominante auflöst. Für den übermäßigen Quintsextakkord als Sixte ajoutée hingegen bleibt die Auflösung über einen plagalen Fundamentschritt (Quintstieg bzw. Quartfall) mit Aufwärtsbewegung der alterierten Sexte charakteristisch:

Das Notenbeispiel oben zeigt bei a) eine nicht-alterierte Sixte ajoutée mit der charakteristischen Auflösung. Bei b) ist die Sixte ajoutée g zu gis bei gleichbleibenden Auflösungsakkord hochalteriert worden. Das Beispiel c) zeigt hingegen die Auflösung des gleichen Akkordes (b-d-f-gis) als übermäßigen Quintsextakkord in d-Moll mit doppeldominantischer Funktion im Sinne der Funktionstheorie (e-gis-h-d-f ohne Grundton e und mit tiefalterierter Quinte h). Die Quintparallelen (b-f zu a-e), die im 18. Jahrhundert bei der Auflösung zur Dominante auftreten können (zwischen b-a im Bass und f-e im Alt, die sogenannten Mozartquinten), sind im Beispiel d) durch einen Quartsextvorhalt vermieden worden. In der Motette »Warum ist das Licht gegeben den Mühseligen« op. 74, Nr. 1 setzt Johannes Brahms den subdominantischen übermäßigen Quintsextakkord kurz vor Ende des Satzes als Steigerungsmittel vor der letzmaligen »Warum«-Frage ein:

Aufgabe 7

Löse die folgenden Akkorde auf als: