Die Kadenz (als Schlusswendung)
In diesem Tutorial wird eine kontrapunktische Perspektive auf das Thema Kadenz gewählt, da dieses für ein Verständnis von komponierter Musik verschiedener Jahrhunderte äußerst hilfreich ist. Erklärungen, die eine Kadenz als Abfolge von Akkorden beschreiben (hierzu wird in der Regel die Stufen- oder Funktionstheorie bemüht), haben ihre Wurzeln in der Stufen- oder Funktionstheorie, also im Beschreibungsmethoden des 19. und frühen 20. Jahrhundert. Obgleich Erklärungen der Kadenz über Akkorde in der Musikpädagogik sowie älteren musiktheoretischen Lehrbüchern verbreitet sind, ist es für ein angemessenes Verständnis problematisch, eine Kadenz auf die Abfolge von Akkorden zu reduzieren.
- Die Kadenz in der Zweistimmigkeit
- Der Leitton
- Die phrygische Kadenz in der Mehrstimmigkeit
- Die ›doppelte‹ Kadenz (cadenza doppia)
- Der Halbschluss (clausula dissecta)
- Zur Didaktik der Kadenz
- Zusammenfassung (Video)
Tenor- und Sopranklausel
Das erste Beispiel zeigt die beiden wichtigsten zweistimmigen Klauseln (Sopranklausel und Tenorklausel), aus denen sich die mehrstimmigen Kadenzen tonaler Musik entwickelt haben. Die einzelnen Stationen im zeitlichen Ablauf der Kadenzen wurden eigens benannt: Antepenultima (drittletzter Ton), Penultima (vorletzter Ton) und Ultima (Schlusston)
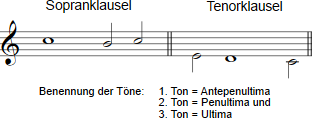
Um zu verstehen, warum mehrstimmige Kadenzen, wie wir sie aus Musik kennen, die zwischen 1500 und 1900 komponiert worden ist, ist es wichtig zu wissen, dass früher die Intervalle in Konsonanzen und Dissonanzen eingeteilt worden sind. Das lässt sich gut anhand einer Obertonreihe und Proportionszahlen veranschaulichen:

Die Obertonreihe und auch die Proportionszahlen für Intervalle sind »natürlich« und können naturwissenschaftlich überprüft werden. In der Natur vorgegeben ist jedoch nicht die Bewertung der Intervalle, welche als ›gut‹ (konsonant) und welche als ›schlecht‹ (dissonant) zu bezeichnen haben. Dass ein Intervall wie die Oktave (2:1), deren Proportionszahl nahe an der ›eins‹ (Unität/Gott) liegt, als ›gut‹ und ein Intervall wie die Septime (16:9) folgerichtig als ›schlecht‹ empfunden worden ist, entspringt einem theologisch-mathematischen Denken, das für den den abendländischen Kulturkreis charakteristisch ist.
Das nächste Beispiel zeigt die Mechanik einer zweistimmigen Klausel (bzw. Kadenz). In ihr gibt es jeweils ein ›schlechtes‹ Intervall (Septime oder Sekunde), das in ein ›besseres‹ (Sexte oder Terz) aufgelöst und in ein ›perfektes‹ Intervall (Oktave, Einklang) überführt (»perfiziert«) wird:

In der Vorstellung einer Kadenz kommt somit eine Spannung zur Ruhe, was sich auch theologisch interpretieren ließ (Erlösungsgedanke). Gleichzeitig ist eine Analogie zur Sprache gesehen worden, weil man das Senken der Stimme und die Pause am Satzende (Punkt) sowie am Satzeinschnitt (Doppelpunkt, Komma) als Ruhe und den gesprochenen Satz vor diesen Zäsuren demgegenüber als Spannung verstand.
In dem folgenden Notenbeispiel ist dieser Sachverhalt sehr schön zu sehen. Hinter dem »est« des Magnificat-Textes »Quia fecit mihi magna, qui potens est: et sanctum nomen eius.« findet sich ein Doppelpunkt. Jacobus Vaet (1529–1567) komponierte in einer Vertonung dieses Textes genau an dieser Stelle eine zweistimmige Kadenz:

Dreistimmige Kadenzen
Diese bereits vollgültigen zweistimmigen Schlusswendungen können nun in der Dreistimmigkeit mit unterschiedlichen Basswendungen (contratenor bassus) versehen werden, wobei der abschließende Quintsprung als Bassklausel bezeichnet wird. Durch die Dreistimmigkeit entsteht dabei eine Harmonik, deren Stationen heute gebräuchlicher Weise als 1. Tonika-Sextakkord, 2. als Dominant-Quartvorhalt, Subdominante oder Doppeldominante, 3. als Dominante und 4. als Tonika bezeichnet werden.

Die Schlusswirkung dieser Kadenzen hängt dabei nach wie vor an der Dynamik der zweistimmigen Klausel, die in den drei Beispielen in den oberen beiden Stimmen vollkommen gleich ist. Gegenüber dieser Konstante sind der Bass und die Harmonik variabel; sie ›beleuchten‹ die zweistimmige Kadenzen auf unterschiedliche Art und Weise (bringen aus heutiger Sicht subdominantische oder dominantische Farben ins Kadenzgeschehen).
Aus dieser Perspektive wird verständlich, warum in einem Trugschluss die Terz verdoppelt werden soll:

Der Grund ist ein musikalischer: Die Terz ist der (verdoppelte) Schlusston der zweistimmigen Kadenz. Durch den Bass, der die Kadenz in den Schlusston nicht mitvollzieht, wird aus harmonischer Sicht eine (verdoppelte) Terz. Ein solches Fliehen des Basses vor der Kadenz wurde früher als »fuggir la cadenza« bezeichnet. Die heute nicht selten zu hörende Begründung, die Terz müsse im Trugschluss verdoppelt werden, damit Parallelen vermieden werden könnten, ist schlichtweg falsch.
Vierstimmige Kadenzen
Im folgenden Beispiel sehen Sie die Benennung der Stimmen in der Standard-Kadenz (links) und originaler Stimmlage sowie eine Kadenz mit Klauseltausch (rechts):

Die Altklausel konnte dabei in drei Formen auftreten: mit einer Tonwiederholung, einem Terzsprung abwärts oder − wenn die Tenorklausel im Bass liegt − mit einem Sekundschritt abwärts (diese Altklausel hat dann die gleichen Töne wie die phrygische Tenorklausel). Die Tonwiederholung kann dabei mit einer regulären Tenorklausel (Sekundschritt abwärts) zu einem Schlussklang ohne Terz, der Terzsprung abwärts mit der Bassklausel im Bass zu einem Schlussklang ohne Quinte führen. Angesichts der verschiedenen Formen der Altklausel lässt sich ganz pragmatisch sagen: In einer vierstimmigen Kadenz lassen sich im Allgemeinen drei Stimmen (Sopran-, Tenor- und Bassklausel) relativ sicher bestimmen, wobei als Altklausel dann jene Stimme bezeichnet werden kann, die in der Vierstimmigkeit übrig bleibt.
Die Tenorklausel gibt es in zwei Formen: In einer älteren Form mit einem Sekundschritt abwärts und in einer neueren mit einem Sekundschritt aufwärts. Der Sekundschritt aufwärts dürfte aus klanglichen Gründen eingeführt geworden sein, um einen vollständigen Schlussklang zu erhalten (in der Altklausel erklingt dazu die Tonwiederholung).
Die Bassklausel in einer oberen Stimme
Wenn in einer vierstimmigen Kadenz die Tenorklausel im Bass liegt, gibt es unterschiedliche Auffassungen hinsichtlich der Bennung der Stimmen:

Denn der als Bassklausel bezeichnete Quintsprung in der Sopranstimme wird manchmal auch als abspringende Tenorklausel gekennzeichnet. Begründet wird diese Bezeichnung damit, dass in der Paenultima dieser Klausel der gleiche Ton (d'' wie in der Tenorklausel (Bass) zu hören ist und abspringend, weil nach diesem d nicht die Finalis c erreicht, sondern in das g ›abgesprungen‹ wird. Diese Benennung könnte sich auf Gallus Dressler stützen, der die Bassklausel vom Klauseltausch explizit ausgenommen hat.
Melodisch hingegen lässt sich der Quintsprung auch als Bassklausel in einer Oberstimme bezeichnen (diese Benennung wird hier bevorzugt). Auch hierfür lassen sich historische Zeugnisse anführen (z.B. Johannes Nucius 1613 und Conradus Matthaei 1652). Das Argument, eine Bassklausel müsse in den Grundton des Schlussklangs führen, überzeugt wenig, weil das in bestimmten Formen der vierstimmigen phrygischen Kadenz auch nicht zutreffend ist. Jedoch müsste angenommen werden (und Nucius sowie Matthei scheinen das getan zu haben), dass die Bassklausel auch mit einem anderen Ton als der Finalis enden darf. Unabhängig davon, wie man sich bei der Benennung entscheidet: der in der zweiten Auflage des Lexikons Die Musik in Geschichte und Gegenwart verallgemeinernde Satz, die »clausula bassizans sollte nach dem Willen der Theoretiker nicht versetzt werden« (MGG, 2. Aufl., Bd. 5 »Kas−Mein«, Sp. 274), ist in dieser absoluten Form leider falsch.
Der Leitton
Entgegen einem weiteren Vorurteil erklangen früher Kadenzen auf allen Tonstufen mit einem Leitton. Der Leitton konnte dabei von unten oder auch von oben in die Finalis führen. In den Tonarten, in denen sie nicht auf natürliche Weise vorhanden waren, findet man sie zwar meistens nicht in den Noten, aber sie wurden von den Sängern um der Schönheit willen improvisierend gesungen (bzw. pulchritudinis causa stillschweigend ergänzt).

Denken Sie daran, dass in der pythargoräischen Stimmung die große Sexte vor der Schlussoktave größer als eine schwebungsfreie reine oder auch als unsere heutige gleichstufig temperierte Sexte klingt, sie also ›nervöser‹ wirkte als heute und der Übergang in die Oktave daher wie eine Auflösung klang. Und die Regel, dass in den Tonfolgen a-g-a, g-f-g und d-c-d (also in den Sopranklauseln, in denen kein natürlicher Halbtonschritt vorhanden ist) ein Leitton improvisiert werden soll, galt dabei anscheinend nicht nur für mehrstimmige Musik, sondern sogar für den ›simplice cantu‹ (also den Choral):


Anonymus »Ars discantus secundum Johannem de Muris«,
Vorlesungsnachschrift wahrscheinlich aus dem 15. Jahrhundert)
In guten Notenausgaben werden solche Vorzeichen über der Note angezeigt, wodurch ersichtlich wird, dass sie sich zwar nicht im originalen Notentext finden, mit großer Wahrscheinlichkeit aber dennoch gesungen worden sind. Alle Kadenzen werden dabei durch einen aufwärtsführenden Leitton charakterisiert mit einer einzigen Ausnahme: In der phrygischen Kadenz führt der Leitton von oben in den Grundton abwärts (f−e).
Die phrygische Kadenz in der Mehrstimmigkeit
In der Mehrstimmigkeit hat die phrygische Kadenz daher auch eine ganz eigene Entwicklung eingeschlagen: Während aus allen anderen Kadenzen der ›authentische Ganzschluss‹ hervorgegangen ist, hat sich aus der phrygischen Kadenz a) der ›plagale Ganzschluss‹ sowie b) eine charakteristische Art des Halbschlusses − der sogenannte phrygische Halbschluss (bzw. die phrygische Wendung) − entwickelt, der häufig für die Vertonung eines Fragens im Text verwendet worden ist:

Die ›doppelte‹ Kadenz (cadenza doppia)
Eine besondere Form der Kadenz war die ›cadenza doppia‹, von der es mehrere Varianten gibt. Der Name ›doppia‹ dürfte verständlich sein, wenn man bedenkt, dass diese Kadenz fast doppelt so lang ist wie eine einfache Kadenz.

Achten Sie in dem ersten Beispiel (links) darauf, dass die Quarte c zum Bass in der zweiten Takthäfte des ersten Taktes als ›konsonante‹ angesehen wurde und daher verdoppelt werden durfte. Die Quarte c zum Bass auf der Takteins des zweiten Taktes (dissonante Patiensstimme zum d der Tenorklausel) durfte hingegen nicht verdoppelt werden.
Besonders reizvoll klingt die cadenza doppia, wenn sie auf einen Ton zielt, der natürlicher Weise eine ›weiche‹ Terz über sich hat (im nächsten Beispiel das a, wobei die Terz c natürlich im Schlussklang ›pulchritudinis causa‹ zur ›harten‹ Terz aufgehellt werden kann). In diesem Fall war es im 17. Jahrhundert sehr beliebt, anstelle der eingangs erklingenden Septimensynkope eine Sexte (zum Bass) zu setzen, wodurch aus heutiger Perspektive ein übermäßiger Dreiklang erklingt:


Beachten Sie, dass Sexten (zum Bass) konsonant sind, diese also auch in der oben gezeigten Wendung angesprungen und verdoppelt werden dürfen (die Septime an dieser Position ist hingegen eine Dissonanz und darf daher weder angesprungen noch verdoppelt werden). Im Beispiel rechts erklingt nach dem ›übermäßigen Dreiklang‹ sogar noch eine weitere Dissoanz, die durch einen betonten dissonanten Durchgang, einen sogenannten Quasi-Transitus ensteht (wenn Sie die Abbildung berühren, können Sie sehen, wie diese Wendung ohne Durchgang aussehen würde).
In einem Madrigal von Robert Ramsay wird die ›cadenza doppia‹ mit ›übermäßigem Dreiklang‹ sogar sequenziert, um mit Tränen »Marmor« zum Schmelzen zu bringen:

Copyright Info: Ensemberlino Vocale, Ltg. Ulrich Kaiser
(Live-Mittschnitt aus einem Konzert in Berlin 1997), CC BY-SA.
Auch in Verbindung mit dem fuggir la cadenza findet sich der ›übermäßige Dreiklang‹ recht häufig und kann daher als ein Stilmittel der Schreibweise nach »Italian Madrigalischer Manier« (Schein) gelten.
Der Halbschluss (clausula dissecta)
Ob aus moderner Perspektive eine Kadenz wie ein Ganzschluss oder als Halbschluss wirkt, ist nur zu einem geringen Teil eine Sache der Satztechnik. Denn in erster Linie entscheidet der Tactus bzw. die Metrik darüber, ob ein Schluss vollkommen schließend oder öffnend klingt. Beim Berühren der Abbildung sehen Sie, dass die Satztechnik im Halb- und Ganzschluss gleich bleiben kann, nur dass im Halbschluss aus heutiger Sicht die Dominante auf schwerer Zeit erklingt und der Schlussklang fehlt:


Erst im 19. Jahrhundert werden Dominanten in einer Kadenz als schweres Ereignis zelebriert (und Schlussklänge gerne leicht abphrasiert). Aus Sicht einer historischen Satztechnik sind der subdominantische Klang, der Quartvorhalt sowie der Schlussklang in der Kadenz Ereignisse auf der Tactuszeit bzw. metrisch schwere Ereignisse, wohingegen die Dominante ein metrische leichte Position in der Kadenz hat (die ›leichte‹ Auflösungsstation nach der Dissonanz auf schwerer Zeit in der Synkopenklausel einer zweistimmigen Kadenz).
Zur Didaktik der Kadenz in der Schule
In der Schule besteht das Problem darin, dass theoretische Erläuertungen erst dann sinnvoll erscheinen, wenn eine Klangvorstellung dafür da ist, was in tonaler Musik als Kadenz bezeichnet wird. Hierfür ist es empfehlenswert, praktisch mit einem Kanon zu beginnen, dem sich dann Erklärungen zu einfachen Kadenzbildungen anschließen können.
Zusammenfassung
Wenn Sie möchten, können Sie eine Zusammenfassung der wichtigsten Informationen zur Kadenz auch als Video anschauen:
Quelle: YouTube.
Literatur und Weblinks:
- Ulrich Kaiser, Die Kadenz als Schlusswendung und Formmodell, OER-Materialien (PDF) zur Kadenz.
- Ulrich Kaiser, Klangverbindungen in der Kadenz (Arbeitsbogen), OER-Materialien (PDF) zur Kadenz.
- Ulrich Kaiser, Gehörbildung. Satzlehre, Improvisation, Höranalyse. Ein Lehrgang mit historischen Beispielen, Kassel 1998, 2 Bde., Bd. I S. 201−209 und Bd. II S. 367−383.
- Ulrich Kaiser, Der vierstimmige Satz. Kantionalsatz und Choralsatz, Kassel 2002, S. 31−63.
- YouTube-Kanal zur Musik um 1600.
Erstellung des Beitrags: 1. April 2013
Letzte Änderung des Beitrags am 3. August 2019