Sequenzen und die Funktionstheorie

von Ulrich Kaiser

In der »Funktionellen Harmonielehre« von Hugo Distler von 1940 findet sich eine Aufgabe (Kapitel XVII, Aufg. 1), in welcher der folgende Bass mit Hilfe von Funktionssymbolen ausgesetzt werden soll:

Es ist schwierig, sich über die Funktionszeichen die konkreten Klänge vorzustellen. Darüber hinaus geben die Funktionssymbole keine Auskunft zur Stimmführung, so dass ein Arbeitsweg nach Distlers Harmonielehreaufgabe für Ungeübtere darin bestanden haben dürfte, sich zuerst über die Funktionssymbole die richtigen Töne zu suchen und anschließend für diese Töne eine korrekte Stimmführung zu überlegen. Das folgende Notenbeispiel zeigt eine mögliche Lösung für Distlers Aufgabe:

Das Ergebnis ist ein gängiges Sequenzmodell (Quintfallsequenz), das mit einer Kadenz beschlossen wird. Diese Sequenz hätte auch wie folgt chiffriert werden können:

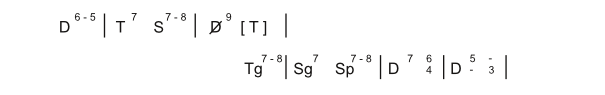
In diesen beiden alternativen Lösungen besteht ein Problem darin, dass dem D⁹-Akkord ohne Grundton im zweiten Takt keine Tonika, sondern ein Tonikavertreter folgt. Da streng genommen die Funktion der Dominante die Erwartung einer Tonika erzeugt, muss der Eintritt des Tonikagegenklangs (Tg) als Trugschluss im weiteren Sinne bezeichnet und die enttäuschte Erwartungshaltung durch eckige Klammern [T] zum Ausdruck gebracht werden. Doch die Regelmäßigkeit der Quintfallsequenz und ihre Voraushörbarkeit widerspricht der Kennzeichnung als Trugschluss. Darüber hinaus lässt sich noch ein weiteres Problem für alle drei angegebenen Funktionschiffrierungen benennen: In der Funktionstheorie weisen Akkorde im Sekund- und Quintabstand eine funktionale Differenz auf, Akkorde im Terzabstand tendieren hingegen zur funktionalen Identität:

In jeder Chiffrierung einer Quintfallsequenz durch Funktionssymbole tritt jedoch an einer Stelle für zwei Akkorde im Quintabstand eine gleiche Funktionalität auf (D−Dp im ersten, Tg−Tp im zweiten und Sg−Sp im dritten Beispiel). Um dieses Problem zu umgehen, wird nicht selten zur Beschreibung von Sequenzen auf die Verwendung von Funktionssymbolen verzichtet und auf Stufensymbole ausgewichen. Mit Hilfe von Stufensymbolen lassen sich die Akkorde ebenfalls chiffrieren, jedoch ohne eine funktionale Deutung der Klänge vornehmen zu müssen:

Eine weitere Beschreibungsmöglichkeit besteht darin, die oben gezeigte Klangfolge als mehrstimmige Ausformung eines elementaren Stimmführungsmodells aufzufassen (Quintfallsequenz mit 7-6-Synkopenkette). Diese Sichtweise verdankt sich in erster Linie Impulsen der historischen Musikwissenschaft, wie sie in der zweiten Hälfte des vergangenen Jahrhunderts von den Musikwissenschaftlern Ernst Apfel und Carl Dahlhaus ausgegangen sind:

Neu an dieser Sichtweise war die Vorstellung, dass satztechnische Modelle eine ›Geschichte‹ haben und − darin vergleichbar der Sprache − wandelbar sind. Wie in der Sprachforschung liegt es daher auch in der Musikforschung nahe, diese Wandlungen zu untersuchen und aus den zu Tage tretenden Unterschieden stilistische und ästhetische Erkenntnisse zu gewinnen. Das satztechnische Modell der 7−6-Synkopenkette ist also nicht nur für die musikalische Analyse der Werke von Arcangelo Corelli, Johann Sebastian Bach und Wolfgang Amadé Mozart geeignet, sondern kann auch zur Beschreibung ›romantischer‹ und expressiv-chromatischer Harmoniefolgen wie zum Beispiel in der Mazurka op. 6 Nr. 1 in fis-Moll von Frédéric Chopin herangezogen werden. Eine Voraussetzung dafür ist allerdings, dass die Vorzeichen ab Takt 5 in einem ursprünglichen Sinne als Chromatisierung bzw. Verfärbung (griech. χρομα = Farbe) eines nicht-chromatischen (diatonischen) Gerüstsatzes verstanden werden:

Das satztechnische Modell der 7-6-Synkopenkette ist hier nicht nur beim Verständnis der Harmonik hilfreich, sondern verdeutlicht auch den Spannungsverlauf des Abschnitts, denn die Mechanik der 7−6-Synkope verursacht eine Bewegung, die erst in der Oktave der fis-Moll-Tonika bzw. der thematischen Wiederholung der Anfangstakte zur Ruhe kommt.
Die Art der Chromatik, also warum die Vorzeichen von Chopin genau in dieser Abfolge und nicht in einer anderen Anordnung verwendet worden sind, vermag das Satzmodell nicht zu erklären. Für diesen Aspekt können wiederum die Funktionssymbole hilfreich sein.

Aufgabe 1

Analysiere mit Hilfe von Funktionssymbolen:

Dem Anfang der Mazurka liegt eine Sequenz zugrunde, die sich wie folgt durch Funktionssymbole chriffrieren lässt:

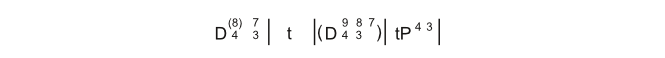
Die Sequenz des Anfangs lässt sich auch wieder über ein Satzmodell beschreiben (immanente Terzparallelen mit Zick-zack-Bass cis-fis-e-a). Dieses Satzmodell ist das als »Pachelbel«-Modell bekannt geworden (es liegt dem berühmten Kanon von Pachelbel zugrunde) und wird in der Fachsprache auch als Parallelismus bezeichnet. Der ganze Anfang bzw. die Takte 1–10 der Mazurka Chopins können daher auch mithilfe des folgenden Gerüstsatzes (Parallelismus und Quintfallsequenz) beschrieben werden:

In der Praxis wird − insbesondere im Umgang mit Sequenzen − die Funktionstheorie heute oftmals als unzureichend empfunden. Ein Vorteil der Beschreibung von Sequenzen über Satzmodelle besteht darin, dass in der Analyse von Anfang an mit einfachen Notenbildern (Gerüstsätzen) gearbeitet werden kann. Das erleichtert wiederum die Ausbildung einer Klangvorstellung für musikalische Phänomene, die sich über abstrakte Chiffrierungssysteme nur ungleich schwieriger erlernen lässt.